X-ray Imaging Systems
In order for any optical system to form an image, it must satisfy the
"Abbe sine condition", at least approximately. The Abbe sine
condition states that an optical system will form an image of an infinitely
distant object only if for each ray in the parallel beam emanating from
the source:
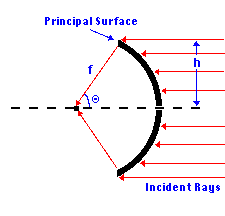
| h/sin(theta) = f |
|
Figure 1
|
|
where h is the (radial) distance of the ray from the optical axis, theta
is the angle of the final path of the ray relative to its initial path
(and thus the optical axis) and f is a constant for all rays. In other
words, an image will be formed if the principal surface, defined as the
locus of intersections of the initial and final paths of rays, is
spherical. An optical system satisfying the Abbe sine condition thus
acts as a simple spherical lens.
|
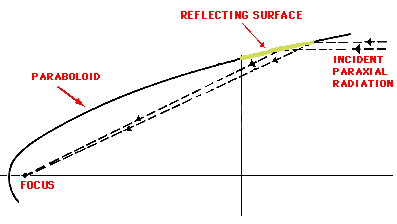
| Figure 2 - A simple parabolic mirror |
A simple parabolic mirror was originally proposed in 1960 by Riccardo
Giacconi and Bruno Rossi, the founders of extrasolar X-ray astronomy. This
type of mirror is often used as the primary reflector in an optical telescope.
However, it does not satisfy the Abbe sine condition, since the principal
surface is the paraboloid itself (see Figure 2).
Paraxial rays (rays impinging on the mirror parallel to the optical axis) will
indeed focus to a point, but images of off-axis objects will be severely
blurred. (An optical reflecting telescope gets around this by use of a
secondary lens to correct this blurring.) The German physicist Hans Wolter
showed in 1952 that the reflection off a combination of two elements, a
paraboloid, followed by a confocal and coaxial paraboloid, will allow the Abbe
sine condition to be nearly satisfied. Wolter also showed that any odd number
of coaxial conic sections will not form an image, but any even number can.

|
Figure 3 - Two element reflection image system
|
Another system which forms real images consists of a set of two orthogonal
parabolas of translation, off which incident X-rays reflect successively,
as first proposed in 1948 by Kirkpatrick and Baez. A simplified
Kirkpatrick-Baez design in shown in Figure 4a. In practical designs, the
surface area is increased by using many approximately parallel mirrors
(i.e., nesting) in each reflecting stage as in Figure 4b. The
Kirkpatrick-Baez system offers inexpensive construction since the reflecting
surfaces can be optically flat glass plates, bent to the proper curvature by
mechanical stressing. On the other hand, the coalignment of many reflecting
surfaces to form an optimum image is a difficult process. Since this was the
first imaging telescope used for non-solar X-ray astronomy, the
Kirkpatrick-Baez system is worthy of mention if only for historical reasons.
The most commonly used X-ray mirrors are the cylindrically symmetric systems
first described by Wolter.

|
Figure 4 - The Kirkpatrick-Baez X-ray Telescope Design
|
|
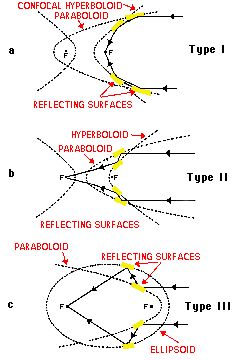
Wolter described three different imaging configurations, the Types I, II,
and III, which are depicted in Figure 5. The design most commonly used by
X-ray astronomers is the Type I since it has the simplest mechanical
configuration (Figure 5a). In addition, the Type I design offers the
possibility of nesting several telescopes inside one another, thereby
increasing the useful reflecting area. This is an extremely important
attribute, as virtually all X-ray sources are weak, and maximizing the light
gathering power of a mirror system is critical. For comparable apertures and
grazing angles, the primary advantage of Type II over Type I is that higher
focal plane magnifications are attainable. This is so because the second
reflection is off the outside of a surface, thus allowing longer focal
lengths. However, since off-axis images suffer much more severely from
blurring in Type II configurations, the Wolter Type II is useful only as a
narrow-field imager or as the optic for a dispersive spectrometer. The Wolter
Type III has never been employed for X-ray astronomy. |
|
Figure 5 - The Wolter X-ray Telescope Designs
|
|

|
Show me a movie about imaging X-rays
|
Contributed by Rob Petre of the Laboratory for High-Energy Astrophysics, GSFC
|
